M.R.U Y PROBLEMAS

MOVIMIENTO RECTILINEO UNIFORME.

El movimiento rectilíneo uniforme (m.r.u.), es aquel con velocidad constante y cuya trayectoria es una línea recta. Un ejemplo claro son las puertas correderas de un ascensor, generalmente se abren y cierran en línea recta y siempre a la misma velocidad.

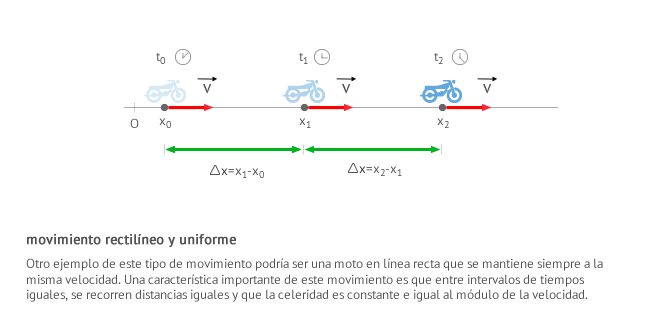
Un movimiento rectilíneo uniforme (m.r.u.) es aquel que tiene su velocidad constante y su trayectoria es una línea recta. Esto implica que:

• El espacio recorrido es igual que el desplazamiento.
• En tiempos iguales se recorren distancias iguales.
• La rapidez o celeridad es siempre constante y coincide con el módulo de la velocidad.

Ecuaciones y Gráficas del M.R.U.

Velocidad

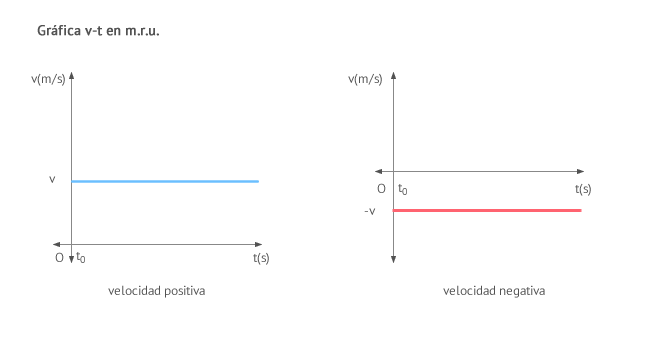
En los m.r.u. la velocidad del cuerpo es constante y por tanto igual a la velocidad inicial. Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s).

v=v0=cte

donde:

• v es la velocidad.
• v0 es la velocidad inicial.

Posición

Su unidad en el Sistema Internacional (S.I.) es el metro (m) y se obtiene por medio de la siguiente expresión:

x=x0+v⋅t

donde:

• x0 es la posición inicial.
• v es la velocidad que tiene el cuerpo a lo largo del movimiento.
• t es el intervalo de tiempo durante el cual se mueve el cuerpo.

Observa lo que t representa en la ecuación de posición: El intervalo de tiempo durante el cual se mueve el cuerpo. Dicho intervalo a veces es representado por t y otras por ∆t. En cualquiera de los casos,  t=∆t = tf - ti siendo tf y ti los instantes de tiempo inicial y final respectivamente del movimiento que estamos estudiando. 

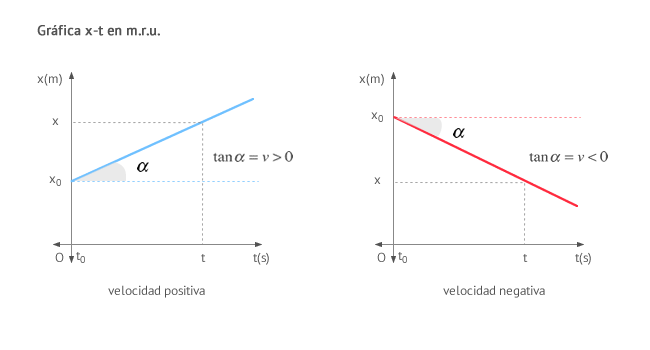
La inclinación de la recta de la gráfica depende de la velocidad. A mayor pendiente, mayor velocidad. Por otro lado, recuerda puedes deducir esta de la gráfica de la fila superior teniendo en cuenta que la distancia recorrida coincide con el área encerrada entre el eje x y la linea que representa la velocidad en el intervalo de tiempo considerado.

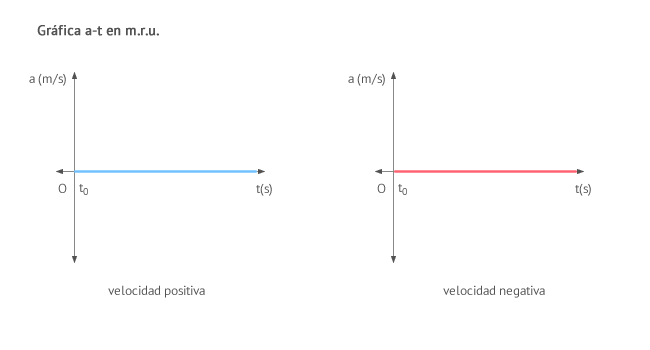
Aceleración

Su unidad en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2). Su valor a lo largo del movimiento siempre es cero.

En aquellos casos en los que la posición inicial es cero ( x0 = 0 ), la distancia recorrida y la posición coinciden, y su valor es:

s=v⋅t

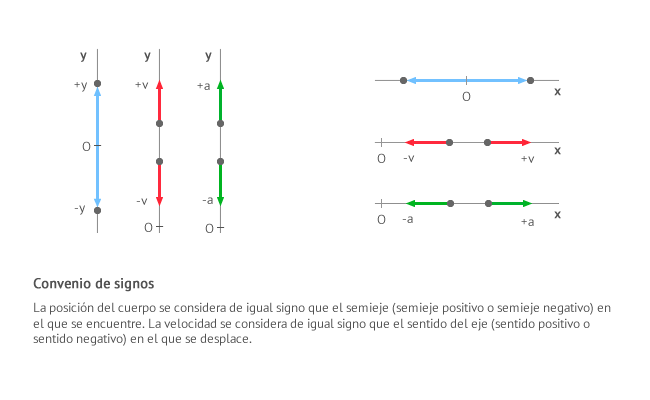
Por último, cuando tengas que usar las ecuaciones anteriores recuerda el siguiente convenio de signos:

• La posición del cuerpo se considera de igual signo que el semieje (semieje positivo o semieje negativo) en el que se encuentre.
• La velocidad se considera de igual signo que el sentido del eje (sentido positivo o sentido negativo) en el que se desplace.

PROBLEMAS SOBRE M.R.U

Si una bola rueda por el suelo describiendo una trayectoria en línea recta y tomamos medidas a cerca de su posición en diferentes instantes de tiempo.

Posición (m)	0	12	24	36
Tiempo (s)	4	25	46	67

La bola realiza un m.r.u.?
b) ¿Cuál es su velocidad?
c) ¿Cuál es su posición transcurridos 8 s?

Solución

Cuestión a)

Para poder establecer si se trata de un m.r.u., deben de cumplirse 2 condiciones:

1. Trayectoria en línea recta
2. Velocidad constante durante todo el movimiento,

El primero se cumple tal y como nos indican en el enunciado, solo nos falta comprobar el segundo.

Dado que, como podemos comprobar en la tabla los datos (muestras), se han ido tomando cada 21 s y durante ese tiempo el cuerpo se desplaza la misma cantidad, es decir, 12 m, es lógico afirmar que durante intervalos de tiempos iguales la bola se desplaza distancias iguales. Por tanto, sin lugar a dudas se trata de un m.r.u.

Cuestión b)

Dado que la velocidad es constante en este tipo de movimientos, podemos calcularla por medio de la definición de velocidad para dos instantantes cualesquiera. Por simplicidad tomaremos los 2 primeros:

Datos

xi = 0 m, xf=12 m
ti = 4 s, tf = 25 s

Resolución

En primer lugar, calcularemos el módulo del vector desplazamiento y el intervalo de tiempo: 

Δr=(xf−xi)2−−−−−−−−√=12 m −0 m = 12 m

Δt=tf−ti=25 s−4 s=21 s

Atendiendo a la definición del módulo de la velocidad:

v=ΔrΔt⇒v=12 m21 s⇒v=0.57 ms/

Cuestión c)

Para calcular su posición a los 8 segundos, deberemos utilizar la ecuación de posición de este tipo de movimientos.

Datos

Posición final del movimiento: x = 0 m.
Tiempo inicial del movimiento: ti = 0 s.
Tiempo final del movimiento: tf = 8 s.
Velocidad: v = 0.57 m/s.

Resolución

Partiendo de la posición 0 m, queremos saber que posición tendrá el cuerpo cuando han transcurrido t = tf-ti = 8 s - 4 s = 4 s. Para ello aplicamos la ecuación de posición en los m.r.u.:

x=x0+v⋅t ⇒x=0 m + 0.57 ms/⋅4 ⇒x=2.28 m